Glass Symmetry from Vectors

This example shows how to identify symmetry (in a glassy system but this could be useful other places) by looking at the angles between 3 vectors in the diffraction pattern at some radial ring in k to identify groups of 3 vectors that are subtended by the same angle.

This is a very simple example with more detailed examples to come.

import pyxem as pxm
from scipy.ndimage import gaussian_filter
import matplotlib.pyplot as plt
import numpy as np

First we load the data and do some basic processing

s = pxm.data.pdnip_glass(allow_download=True)
s.axes_manager.signal_axes[0].offset = -23.7
s.axes_manager.signal_axes[1].offset = -19.3

s.filter(gaussian_filter, sigma=(1, 1, 0, 0), inplace=True)  # only in real space
s.template_match_disk(disk_r=5, subtract_min=False, inplace=True)

vectors = s.get_diffraction_vectors(threshold_abs=0.5, min_distance=3)

  0%|          | 0/17 [00:00<?, ?it/s]
  6%|▌         | 1/17 [00:01<00:20,  1.26s/it]
 18%|█▊        | 3/17 [00:02<00:11,  1.26it/s]
 29%|██▉       | 5/17 [00:03<00:08,  1.41it/s]
 41%|████      | 7/17 [00:05<00:06,  1.48it/s]
 53%|█████▎    | 9/17 [00:06<00:05,  1.52it/s]
 65%|██████▍   | 11/17 [00:07<00:03,  1.54it/s]
 76%|███████▋  | 13/17 [00:08<00:02,  1.56it/s]
 88%|████████▊ | 15/17 [00:10<00:01,  1.57it/s]
100%|██████████| 17/17 [00:10<00:00,  1.68it/s]

  0%|          | 0/33 [00:00<?, ?it/s]
  3%|▎         | 1/33 [00:00<00:26,  1.21it/s]
 15%|█▌        | 5/33 [00:01<00:08,  3.37it/s]
 27%|██▋       | 9/33 [00:02<00:05,  4.04it/s]
 39%|███▉      | 13/33 [00:03<00:04,  4.36it/s]
 52%|█████▏    | 17/33 [00:04<00:03,  4.57it/s]
 64%|██████▎   | 21/33 [00:04<00:02,  4.64it/s]
 76%|███████▌  | 25/33 [00:05<00:01,  4.68it/s]
 88%|████████▊ | 29/33 [00:06<00:00,  4.71it/s]
100%|██████████| 33/33 [00:06<00:00,  4.98it/s]

  0%|          | 0/33 [00:00<?, ?it/s]
100%|██████████| 33/33 [00:00<00:00, 541.04it/s]

Now we can convert to polar vectors

pol = vectors.to_polar()

  0%|          | 0/33 [00:00<?, ?it/s]
 64%|██████▎   | 21/33 [00:00<00:00, 198.81it/s]
100%|██████████| 33/33 [00:00<00:00, 215.50it/s]

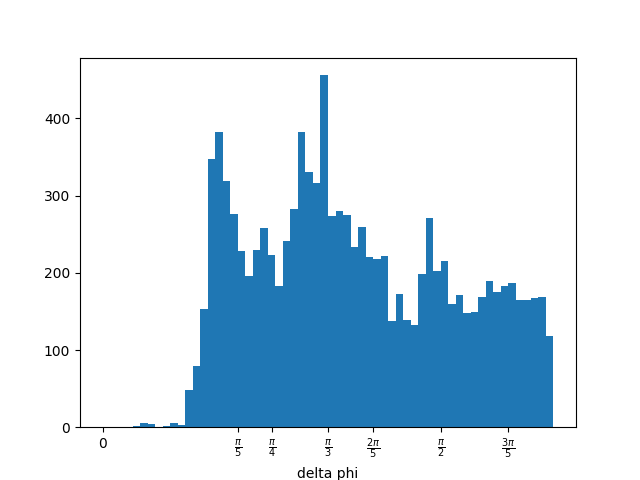
This function gets the inscribed angle accept_threshold is the maximum difference between the two angles subtended by the 3 vectors

ins = pol.get_angles(min_angle=0.05, min_k=0.3, accept_threshold=0.1)

flat_vect = ins.flatten_diffraction_vectors()

fig, axs = plt.subplots()
axs.hist(flat_vect.ivec["delta phi"].data, bins=60, range=(0, 2 * np.pi / 3))
axs.set_xlabel("delta phi")
axs.set_xticks(
    [0, np.pi / 5, np.pi / 4, 2 * np.pi / 5, np.pi / 2, np.pi / 3, 3 * np.pi / 5]
)
axs.set_xticklabels(
    [
        0,
        r"$\frac{\pi}{5}$",
        r"$\frac{\pi}{4}$",
        r"$\frac{2\pi}{5}$",
        r"$\frac{\pi}{2}$",
        r"$\frac{\pi}{3}$",
        r"$\frac{3\pi}{5}$",
    ]
)

  0%|          | 0/33 [00:00<?, ?it/s]
  9%|▉         | 3/33 [00:00<00:01, 22.86it/s]
 21%|██        | 7/33 [00:00<00:00, 26.11it/s]
 30%|███       | 10/33 [00:00<00:01, 22.58it/s]
 39%|███▉      | 13/33 [00:01<00:03,  5.60it/s]
 45%|████▌     | 15/33 [00:01<00:02,  6.60it/s]
 52%|█████▏    | 17/33 [00:02<00:02,  6.40it/s]
 58%|█████▊    | 19/33 [00:02<00:02,  5.29it/s]
 64%|██████▎   | 21/33 [00:03<00:02,  5.26it/s]
 70%|██████▉   | 23/33 [00:03<00:01,  6.44it/s]
 76%|███████▌  | 25/33 [00:03<00:01,  6.45it/s]
 82%|████████▏ | 27/33 [00:04<00:01,  4.35it/s]
 88%|████████▊ | 29/33 [00:04<00:00,  5.14it/s]
 94%|█████████▍| 31/33 [00:04<00:00,  5.29it/s]
100%|██████████| 33/33 [00:04<00:00,  6.72it/s]

  0%|          | 0/2 [00:00<?, ?it/s]
100%|██████████| 2/2 [00:00<00:00, 5336.26it/s]

[Text(0.0, 0, '0'), Text(0.6283185307179586, 0, '$\\frac{\\pi}{5}$'), Text(0.7853981633974483, 0, '$\\frac{\\pi}{4}$'), Text(1.2566370614359172, 0, '$\\frac{2\\pi}{5}$'), Text(1.5707963267948966, 0, '$\\frac{\\pi}{2}$'), Text(1.0471975511965976, 0, '$\\frac{\\pi}{3}$'), Text(1.8849555921538759, 0, '$\\frac{3\\pi}{5}$')]

cycle through colors in groups of 3 for each symmetry cluster

points = ins.to_markers(
    color=["b", "b", "b", "g", "g", "g", "y", "y", "y", "r", "r", "r"]
)
original_points = vectors.to_markers(color="w", alpha=0.5)
s.axes_manager.indices = (67, 55)  # jumping to a part with some symmetric structure

s.plot(vmin=0.0)
s.add_marker(points)
s.add_marker(original_points)

• 
• 

  0%|          | 0/33 [00:00<?, ?it/s]
 67%|██████▋   | 22/33 [00:00<00:00, 218.99it/s]
100%|██████████| 33/33 [00:00<00:00, 216.57it/s]

  0%|          | 0/33 [00:00<?, ?it/s]
100%|██████████| 33/33 [00:00<00:00, 1011.79it/s]

  0%|          | 0/33 [00:00<?, ?it/s]
100%|██████████| 33/33 [00:00<00:00, 1007.63it/s]