Azimuthal Integration (in Pyxem!)

pyxem now includes built in azimuthal integration functionality. This is useful for extracting radial profiles from diffraction patterns in 1 or 2 dimensions. The new method will split the pixels into radial bins and then sum the intensity in each bin resulting in a Diffraction1D or Polar2D signal. In each case the total intensity of the diffraction pattern is preserved.

import pyxem as pxm
import hyperspy.api as hs
import numpy as np

s = pxm.data.tilt_boundary_data()
s.calibration(
    center=None
)  # set the center to None to use center of the diffraction patterns
s.calibration.units = "/AA^{-1}"
s.calibration.scale = 0.03  # To angstroms
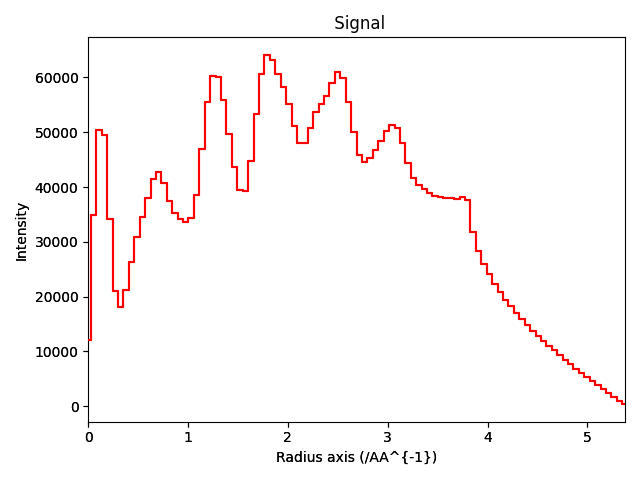
s1d = s.get_azimuthal_integral1d(npt=100, inplace=False)

s1d.sum().plot()

  0%|          | 0/17 [00:00<?, ?it/s]
  6%|▌         | 1/17 [00:00<00:02,  6.01it/s]
100%|██████████| 17/17 [00:00<00:00, 74.34it/s]

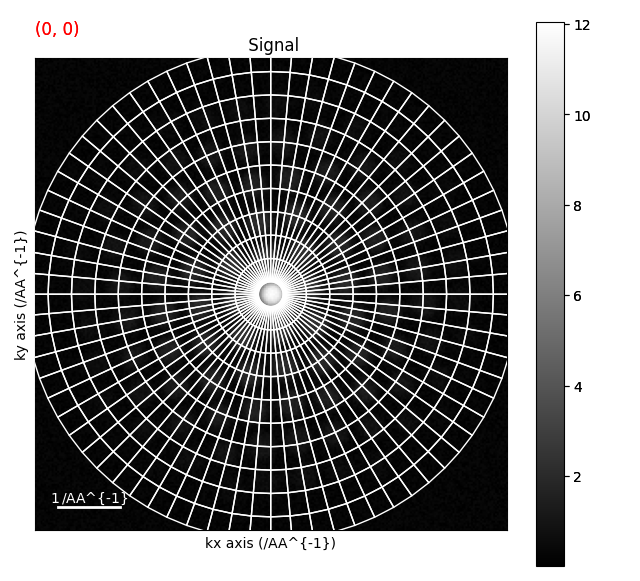
Aside: Actual Implementation Here we have plotted the polygon bins which we use to integrate. For each bin, the pixel indicies contained are saved to an array along side the fraction of each pixel within the bin. Then for each diffraction pattern the fraction of each pixel within the bin is mutiplied, then summed to “integrate” the intensity for each radial bin.

from pyxem.utils._azimuthal_integrations import _get_control_points

cp = _get_control_points(
    10, npt_azim=72, radial_range=(0.2, 4), azimuthal_range=(-np.pi, np.pi), affine=None
)[:, :, ::-1]
poly = hs.plot.markers.Polygons(verts=cp, edgecolor="w", facecolor="none")
s.plot()
s.add_marker(poly)

• 
• 

Similarly, the get_azimuthal_integral2d method will return a Polar2D signal.

s_polar = s.get_azimuthal_integral2d(npt=100, npt_azim=360, inplace=False)
s_polar.sum().plot()

  0%|          | 0/17 [00:00<?, ?it/s]
 82%|████████▏ | 14/17 [00:00<00:00, 130.09it/s]
100%|██████████| 17/17 [00:00<00:00, 137.67it/s]

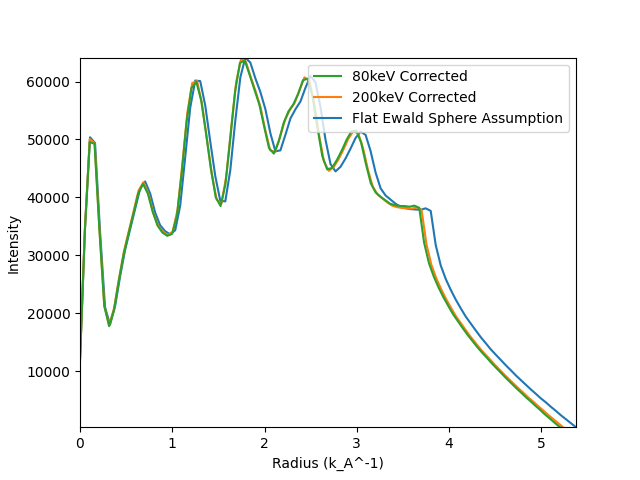
There are also other things you can account for with azimuthal integration, such as the effects of the Ewald sphere. This can be done by calibrating with a known detector distance, and beam energy. In most cases the Flat Ewald sphere assumption is good enough but occasionally, you might want some additional Accuracy.

Here we just show the effect of just calibrating with the first peak vs. calibrating with the known beam energy and detector distance. For things like accurate template matching good calibration can be important when matching to high diffraction vectors. The calibration example gives more information on how to get the correct values for your microscope/setup.

If you are doing x-ray diffraction please raise an issue on the pyxem github to let us know! The same assumptions should apply for each case, but it would be good to test!

We only show the 1D case here, but the same applies for the 2D case as well!

s.calibration.detector(
    pixel_size=0.000092,
    detector_distance=0.125,
    beam_energy=200,
    center=None,
    units="k_A^-1",
)  # set the center= None to use the center of the diffraction patterns
s1d_200 = s.get_azimuthal_integral1d(npt=100, inplace=False)
s.calibration.detector(
    pixel_size=0.000092,
    detector_distance=0.075,
    beam_energy=80,
    center=None,
    units="k_A^-1",
)  # These are just made up pixel sizes and detector distances for illustration

s1d_80 = s.get_azimuthal_integral1d(npt=100, inplace=False)

hs.plot.plot_spectra(
    [s1d.sum(), s1d_200.sum(), s1d_80.sum()],
    legend=["Flat Ewald Sphere Assumption", "200keV Corrected", "80keV Corrected"],
)

  0%|          | 0/17 [00:00<?, ?it/s]
100%|██████████| 17/17 [00:00<00:00, 262.71it/s]

  0%|          | 0/17 [00:00<?, ?it/s]
100%|██████████| 17/17 [00:00<00:00, 261.45it/s]

<Axes: xlabel='Radius (k_A^-1)', ylabel='Intensity'>

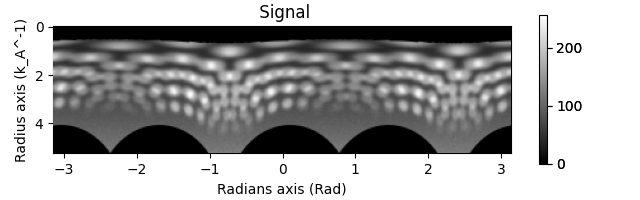
At times you may want to use a mask to exclude certain pixels from the azimuthal integration or apply an affine transformation to the diffraction patterns before azimuthal integration. This can be done using the mask and affine parameters of the Calibration object.

Here we just show a random affine transformation for illustration.

mask = s.get_direct_beam_mask(radius=20)  # Mask the direct beam
affine = np.array(
    [[0.9, 0.1, 0], [0.1, 0.9, 0], [0, 0, 1]]
)  # Just a random affine transformation for illustration
s.calibration(mask=mask, affine=affine)
s.get_azimuthal_integral2d(npt=100, npt_azim=360, inplace=False).sum().plot()

  0%|          | 0/17 [00:00<?, ?it/s]
  6%|▌         | 1/17 [00:04<01:05,  4.08s/it]
100%|██████████| 17/17 [00:04<00:00,  4.09it/s]

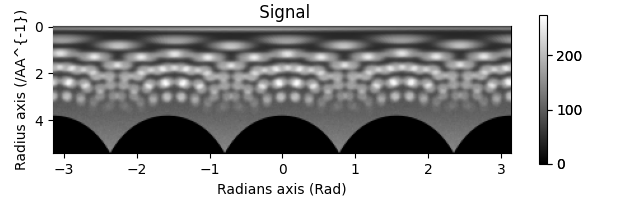
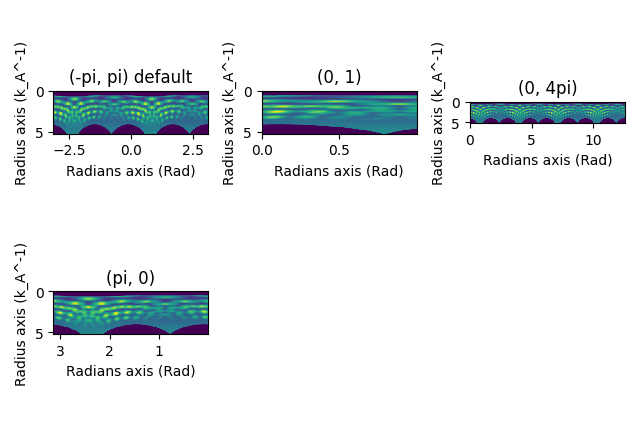
The azimuth_range-argument lets you choose what angular range to calculate the azimuthal integral for. The range can be increasing, decreasing, and does not need to be a multiple of pi.

pol1 = s.get_azimuthal_integral2d(npt=100, azimuth_range=(-np.pi, np.pi))

pol2 = s.get_azimuthal_integral2d(npt=100, azimuth_range=(0, 1))

pol3 = s.get_azimuthal_integral2d(npt=100, npt_azim=720, azimuth_range=(0, 4 * np.pi))

pol4 = s.get_azimuthal_integral2d(npt=100, azimuth_range=(np.pi, 0))

hs.plot.plot_images(
    [pol1.sum(), pol2.sum(), pol3.sum(), pol4.sum()],
    label=["(-pi, pi) default", "(0, 1)", "(0, 4pi)", "(pi, 0)"],
    cmap="viridis",
    tight_layout=True,
    colorbar=None,
)

  0%|          | 0/17 [00:00<?, ?it/s]
100%|██████████| 17/17 [00:00<00:00, 210.10it/s]

  0%|          | 0/17 [00:00<?, ?it/s]
100%|██████████| 17/17 [00:00<00:00, 226.41it/s]

  0%|          | 0/17 [00:00<?, ?it/s]
 71%|███████   | 12/17 [00:00<00:00, 116.81it/s]
100%|██████████| 17/17 [00:00<00:00, 112.22it/s]

  0%|          | 0/17 [00:00<?, ?it/s]
100%|██████████| 17/17 [00:00<00:00, 229.35it/s]

[<Axes: title={'center': '(-pi, pi) default'}, xlabel='Radians axis (Rad)', ylabel='Radius axis (k_A^-1)'>, <Axes: title={'center': '(0, 1)'}, xlabel='Radians axis (Rad)', ylabel='Radius axis (k_A^-1)'>, <Axes: title={'center': '(0, 4pi)'}, xlabel='Radians axis (Rad)', ylabel='Radius axis (k_A^-1)'>, <Axes: title={'center': '(pi, 0)'}, xlabel='Radians axis (Rad)', ylabel='Radius axis (k_A^-1)'>]