Single Phase Orientation Mapping

You can also calculate the orientation of the grains in a single phase sample using the pyxem.signals.PolarSignal2D.get_orientation() method. This requires that you simulate the entire S2 space for the phase and then compare to the simulated diffraction.

For more information on the orientation mapping process see [CCAAnes+22]

from pyxem.data import si_phase, si_grains
from diffsims.generators.simulation_generator import SimulationGenerator
from orix.sampling import get_sample_reduced_fundamental

simulated_si = si_grains()

Pre-Processing

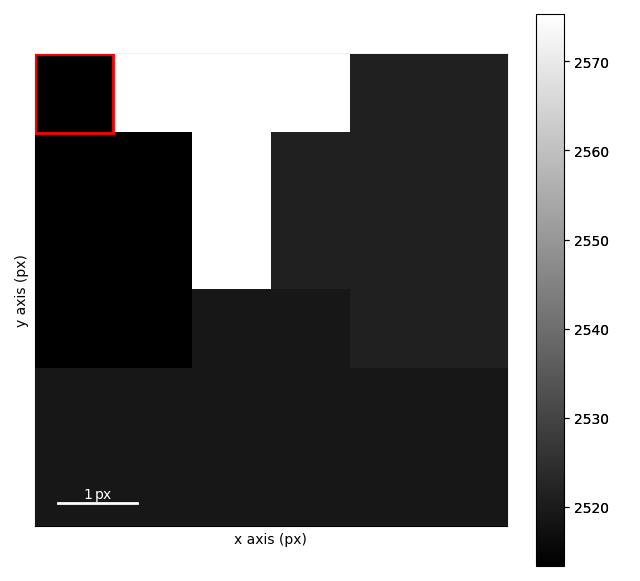
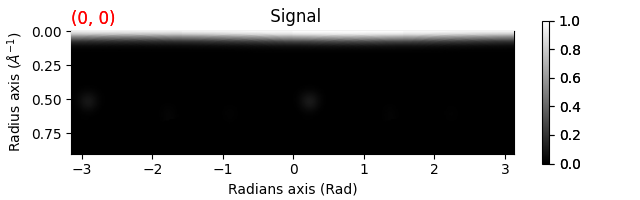
First we center the diffraction patterns and get a polar signal Increasing the number of npt_azim with give better polar sampling but will take longer to compute the orientation map The mean=True argument will return the mean pixel value in each bin rather than the sum this makes the high k values more visible

simulated_si.calibration.center = None
polar_si = simulated_si.get_azimuthal_integral2d(
    npt=100, npt_azim=360, inplace=False, mean=True
)
polar_si.plot()

• 
• 

  0%|          | 0/37 [00:00<?, ?it/s]
  3%|▎         | 1/37 [00:04<02:24,  4.02s/it]
100%|██████████| 37/37 [00:04<00:00,  9.06it/s]

Building a Simulation

Now we can get make a simulation. In this case we want to set a minimum_intensity which removes the low intensity reflections. we also sample the S2 space using the :func`orix.sampling.get_sample_reduced_fundamental`. Make sure that you set with_direct_beam=False or the orientation mapping will be unduely affected by the center beam.

phase = si_phase()
generator = SimulationGenerator(200, minimum_intensity=0.05)
rotations = get_sample_reduced_fundamental(resolution=1, point_group=phase.point_group)
sim = generator.calculate_diffraction2d(
    phase,
    rotation=rotations,
    max_excitation_error=0.1,
    reciprocal_radius=2,
    with_direct_beam=False,
)  # Make sure that with_direct_beam ==False

Getting the Orientation

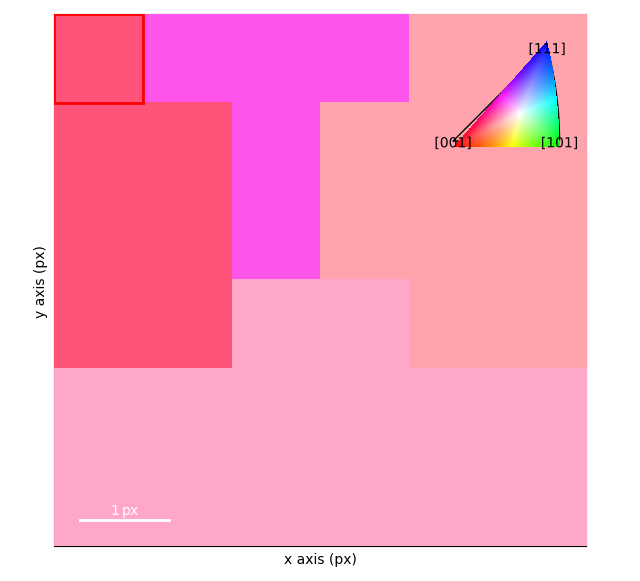
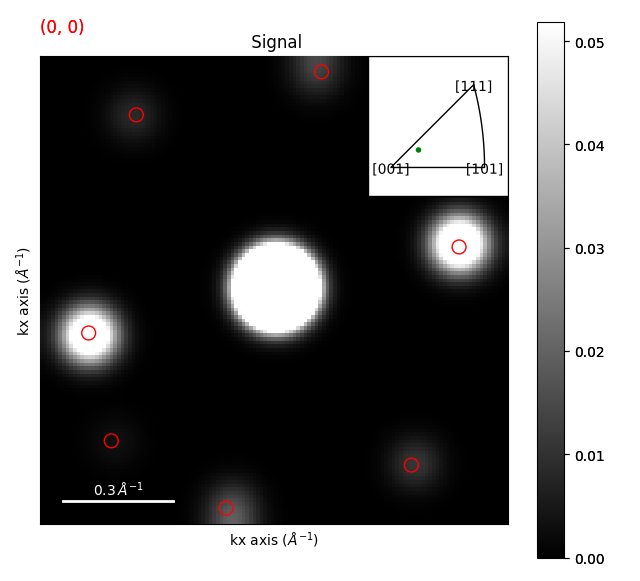
By default the get_orientation function uses a gamma correction equilivent to polar_si**0.5. For noisy datasets it might be a good idea to reduce the noise (Maybe by averaging neighboring patterns?) or simple background subtraction, otherwise the gamma correction will increase the effects of noise on the data. This tries to focus on “Is the Bragg vector there?” rather than “Is the Bragg vector the right intensity?” patially because the intensity of the Bragg vector might have many different effects.

polar_si = polar_si**0.5  # gamma correction.
orientation_map = polar_si.get_orientation(sim)
orientation_map.plot_over_signal(simulated_si, vmax="96th")

• 
• 

  0%|          | 0/73 [00:00<?, ?it/s]
  1%|▏         | 1/73 [00:03<03:45,  3.13s/it]
100%|██████████| 73/73 [00:03<00:00, 22.98it/s]

  0%|          | 0/73 [00:00<?, ?it/s]
100%|██████████| 73/73 [00:00<00:00, 7736.22it/s]

  0%|          | 0/73 [00:00<?, ?it/s]
100%|██████████| 73/73 [00:00<00:00, 7657.09it/s]

  0%|          | 0/73 [00:00<?, ?it/s]
100%|██████████| 73/73 [00:00<00:00, 6784.04it/s]

sphinx_gallery_thumbnail_number = 4