Strain Mapping

Strain mapping in pyxem is done by fitting a DisplacementGradientMap to the data. This can be thought of as image distortion around some central point.

from pyxem.data import simulated_strain
import hyperspy.api as hs

In this example we will create a simulated strain map using the simulated_strain() function. This just creates a simulated diffraction pattern and applies a simple “strain” to it. In this case using simulated data is slightly easier for demonstration purposes. If you want to use real data the zrnb_precipitate() dataset is a good example of strain from a precipitate.

strained_signal = simulated_strain(
    navigation_shape=(32, 32),
    signal_shape=(512, 512),
    disk_radius=20,
    num_electrons=1e5,
    strain_matrix=None,
    lazy=True,
)

The first thing we want to do is to find peaks within the diffraction pattern. I’d recommend using the get_diffraction_vectors() method

strained_signal.calibration.center = (
    None  # First set the center to be (256, 256) or the center of the signal
)
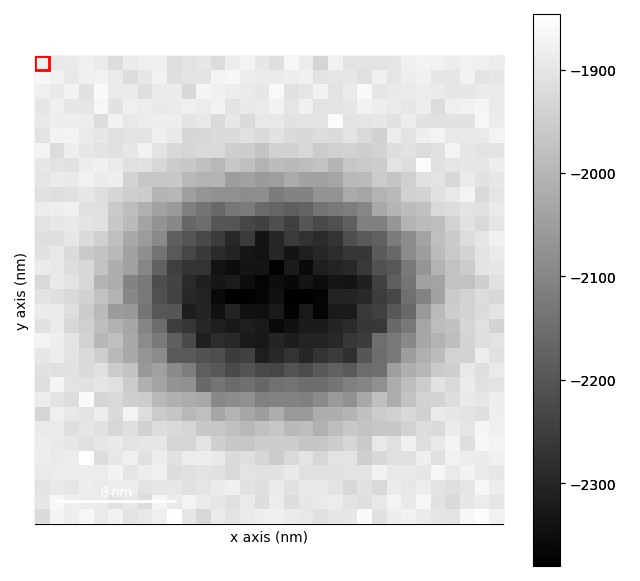
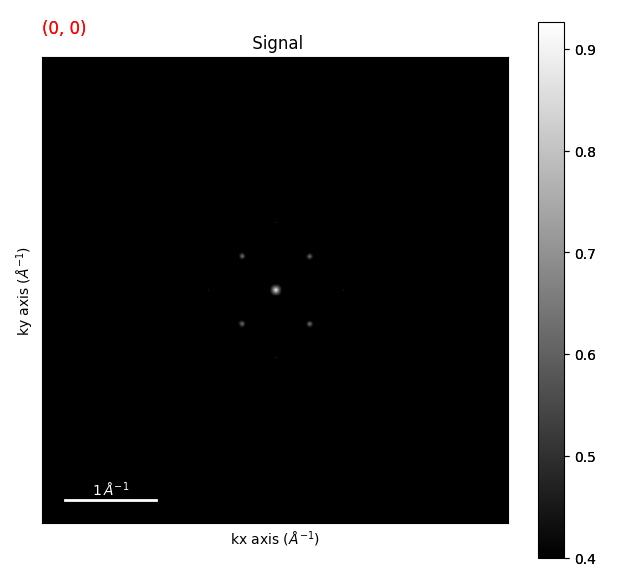
template_matched = strained_signal.template_match_disk(disk_r=20, subtract_min=False)
template_matched.plot(vmin=0.4)

• 
• 

  0%|          | 0/65 [00:00<?, ?it/s]
  2%|▏         | 1/65 [00:00<00:31,  2.04it/s]
  8%|▊         | 5/65 [00:00<00:10,  5.58it/s]
 14%|█▍        | 9/65 [00:01<00:08,  6.72it/s]
 17%|█▋        | 11/65 [00:01<00:06,  8.18it/s]
 20%|██        | 13/65 [00:02<00:07,  6.86it/s]
 26%|██▌       | 17/65 [00:02<00:06,  7.44it/s]
 29%|██▉       | 19/65 [00:02<00:05,  8.40it/s]
 32%|███▏      | 21/65 [00:02<00:05,  7.64it/s]
 35%|███▌      | 23/65 [00:03<00:04,  8.69it/s]
 38%|███▊      | 25/65 [00:03<00:05,  7.96it/s]
 42%|████▏     | 27/65 [00:03<00:04,  8.87it/s]
 45%|████▍     | 29/65 [00:03<00:04,  8.16it/s]
 48%|████▊     | 31/65 [00:04<00:03,  8.96it/s]
 51%|█████     | 33/65 [00:04<00:03,  8.45it/s]
 54%|█████▍    | 35/65 [00:04<00:03,  8.92it/s]
 57%|█████▋    | 37/65 [00:04<00:03,  8.68it/s]
 60%|██████    | 39/65 [00:04<00:02,  8.83it/s]
 63%|██████▎   | 41/65 [00:05<00:02,  8.73it/s]
 66%|██████▌   | 43/65 [00:05<00:02,  8.71it/s]
 69%|██████▉   | 45/65 [00:05<00:02,  8.91it/s]
 72%|███████▏  | 47/65 [00:05<00:02,  8.51it/s]
 75%|███████▌  | 49/65 [00:06<00:01,  9.10it/s]
 78%|███████▊  | 51/65 [00:06<00:01,  8.41it/s]
 82%|████████▏ | 53/65 [00:06<00:01,  9.36it/s]
 85%|████████▍ | 55/65 [00:06<00:01,  8.23it/s]
 88%|████████▊ | 57/65 [00:06<00:00,  9.58it/s]
 91%|█████████ | 59/65 [00:07<00:00,  8.04it/s]
 97%|█████████▋| 63/65 [00:07<00:00,  8.58it/s]
100%|██████████| 65/65 [00:07<00:00,  8.41it/s]

Plotting the template matched signal and setting vmin is a good way to see what threshold you should use for the get_diffraction_vectors() method.

diffraction_vectors = template_matched.get_diffraction_vectors(
    threshold_abs=0.4, min_distance=5
)

markers = diffraction_vectors.to_markers(color="w", sizes=5, alpha=0.5)
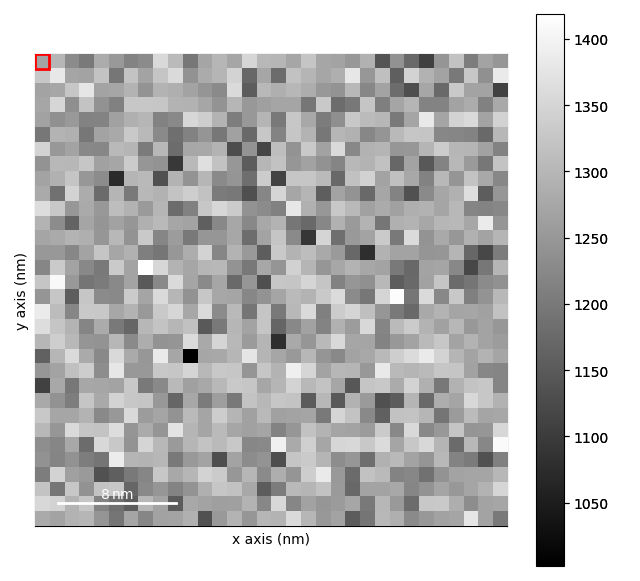
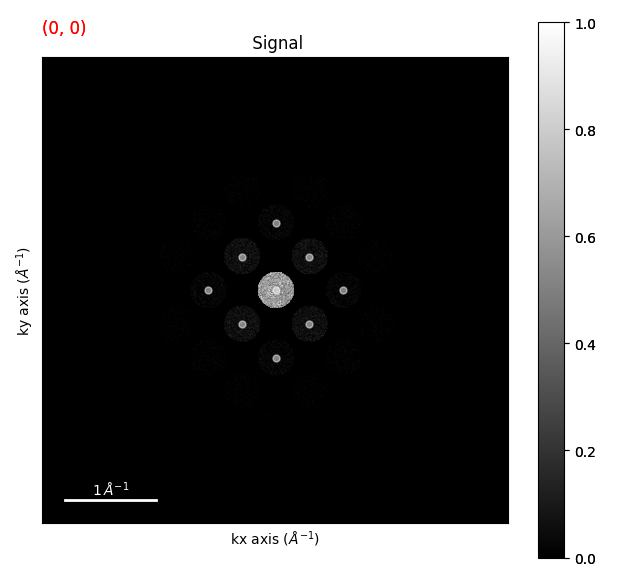
strained_signal.plot()
strained_signal.add_marker(markers)

• 
• 

  0%|          | 0/65 [00:00<?, ?it/s]
100%|██████████| 65/65 [00:00<00:00, 1003.17it/s]

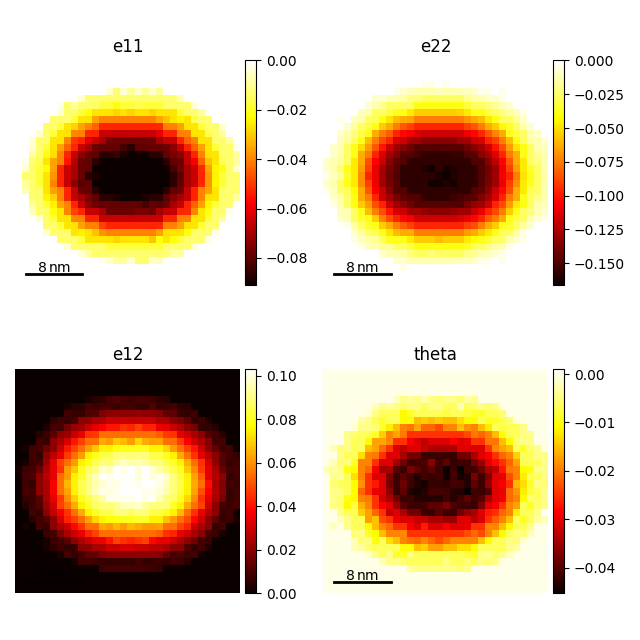
Determining the Strain

We can just use the first ring of the diffraction pattern to determine the strain. We can do this by using the filter_magnitude() method. You can also look at the filtering vectors example to see how to select which vectors you want to use more generally. You can also just manually input the un-strained vectors or use simulated/ rotated vectors as well.

first_ring_vectors = diffraction_vectors.filter_magnitude(
    min_magnitude=0.1,
    max_magnitude=1,
)
unstrained_vectors = first_ring_vectors.inav[0, 0]

strain_maps = first_ring_vectors.get_strain_maps(
    unstrained_vectors=unstrained_vectors, return_residuals=False
)

strain_maps.plot()

  0%|          | 0/2 [00:00<?, ?it/s]
 50%|█████     | 1/2 [00:00<00:00,  1.65it/s]
100%|██████████| 2/2 [00:00<00:00,  3.29it/s]

  0%|          | 0/65 [00:00<?, ?it/s]
  2%|▏         | 1/65 [00:00<00:41,  1.53it/s]
  8%|▊         | 5/65 [00:01<00:14,  4.24it/s]
 14%|█▍        | 9/65 [00:01<00:10,  5.13it/s]
 20%|██        | 13/65 [00:02<00:09,  5.55it/s]
 26%|██▌       | 17/65 [00:03<00:08,  5.80it/s]
 29%|██▉       | 19/65 [00:03<00:06,  6.83it/s]
 32%|███▏      | 21/65 [00:03<00:07,  5.70it/s]
 35%|███▌      | 23/65 [00:04<00:06,  6.77it/s]
 38%|███▊      | 25/65 [00:04<00:07,  5.67it/s]
 42%|████▏     | 27/65 [00:04<00:05,  6.64it/s]
 45%|████▍     | 29/65 [00:05<00:06,  5.69it/s]
 48%|████▊     | 31/65 [00:05<00:05,  6.57it/s]
 51%|█████     | 33/65 [00:05<00:05,  5.75it/s]
 54%|█████▍    | 35/65 [00:06<00:04,  6.51it/s]
 57%|█████▋    | 37/65 [00:06<00:04,  5.82it/s]
 60%|██████    | 39/65 [00:06<00:04,  6.47it/s]
 63%|██████▎   | 41/65 [00:07<00:04,  5.88it/s]
 66%|██████▌   | 43/65 [00:07<00:03,  6.36it/s]
 69%|██████▉   | 45/65 [00:07<00:03,  5.96it/s]
 72%|███████▏  | 47/65 [00:07<00:02,  6.33it/s]
 75%|███████▌  | 49/65 [00:08<00:02,  6.07it/s]
 78%|███████▊  | 51/65 [00:08<00:02,  6.23it/s]
 82%|████████▏ | 53/65 [00:09<00:01,  6.07it/s]
 85%|████████▍ | 55/65 [00:09<00:01,  6.24it/s]
 88%|████████▊ | 57/65 [00:09<00:01,  6.13it/s]
 91%|█████████ | 59/65 [00:09<00:00,  6.15it/s]
 94%|█████████▍| 61/65 [00:10<00:00,  6.17it/s]
 97%|█████████▋| 63/65 [00:10<00:00,  6.19it/s]
100%|██████████| 65/65 [00:10<00:00,  6.12it/s]

  0%|          | 0/33 [00:00<?, ?it/s]
100%|██████████| 33/33 [00:00<00:00, 1009.70it/s]

  0%|          | 0/33 [00:00<?, ?it/s]
100%|██████████| 33/33 [00:00<00:00, 1590.69it/s]

  0%|          | 0/33 [00:00<?, ?it/s]
100%|██████████| 33/33 [00:00<00:00, 7221.75it/s]

  0%|          | 0/9 [00:00<?, ?it/s]
100%|██████████| 9/9 [00:00<00:00, 10252.24it/s]

[<Axes: title={'center': 'e11'}, xlabel='x axis (nm)', ylabel='y axis (nm)'>, <Axes: title={'center': 'e22'}, xlabel='x axis (nm)', ylabel='y axis (nm)'>, <Axes: title={'center': 'e12'}, xlabel='x axis (nm)', ylabel='y axis (nm)'>, <Axes: title={'center': 'theta'}, xlabel='x axis (nm)', ylabel='y axis (nm)'>]

Some final notes about strain mapping. In general, you want to use as many pixels as possible. 512 x 512 is a good place to start. You can do strain mapping with fewer pixels, but the results will be less accurate. Precession also helps improve the results as does having a thinner sample both of which reduce the effects of dynamical diffraction.

sphinx_gallery_thumbnail_number = 5