Fluctuation Electron Microscopy#

This example shows you how to perform a fluctuation electron microscopy (FEM) analysis.

In this example we will focus on calculating \(V_\Omega (k)\) which is defined as,

Equation 1:

\[V_\Omega (k) = \frac{\langle I{^2}(k) \rangle{_r} - \langle I(k)\rangle_r^2}{\langle I(k)\rangle_r^2 } - \frac{G}{\langle I(k)\rangle_r}\]

where \(I(k)\) is the diffracted electron intensity averaged over the polar angle at constant scattering vector magnitude k, \(<>_r\) indicates averaging over probe positions, and G is the gain of the electron camera in counts per electron for counted or data from hybrid pixel detectors this value is 1 otherwise it will be some mean value. The first term is the definition of the variance, and the second term is a correction to the variance for Poisson noise in the data.

(There are several different possible variance signals. Here, we use the notation from Daulton, et al. Ultramicroscopy 110, 1279–1289 (2010), DOI: 10.1016/j.ultramic.2010.05.010.)

import pyxem as pxm
from pyxem.utils import determine_ellipse
import numpy as np
import hyperspy.api as hs
from pyxem.utils._pixelated_stem_tools import _copy_axes_object_metadata

s = pxm.data.zrcual_1(allow_download=True, signal_type="electron_diffraction")
s.plot()

  0%|                                              | 0.00/18.3M [00:00<?, ?B/s]
  0%|                                     | 8.19k/18.3M [00:00<03:45, 80.9kB/s]
  0%|                                      | 39.9k/18.3M [00:00<01:24, 215kB/s]
  0%|▏                                     | 82.9k/18.3M [00:00<01:00, 302kB/s]
  1%|▎                                      | 146k/18.3M [00:00<00:42, 425kB/s]
  1%|▍                                      | 231k/18.3M [00:00<00:31, 567kB/s]
  2%|▋                                      | 299k/18.3M [00:00<00:30, 595kB/s]
  2%|▊                                      | 394k/18.3M [00:00<00:25, 700kB/s]
  3%|█                                      | 476k/18.3M [00:00<00:24, 727kB/s]
  3%|█▎                                     | 606k/18.3M [00:00<00:19, 890kB/s]
  4%|█▌                                     | 705k/18.3M [00:01<00:19, 909kB/s]
  4%|█▋                                     | 803k/18.3M [00:01<00:19, 917kB/s]
  5%|██                                    | 981k/18.3M [00:01<00:14, 1.16MB/s]
  6%|██▎                                  | 1.13M/18.3M [00:01<00:13, 1.24MB/s]
  7%|██▌                                  | 1.25M/18.3M [00:01<00:13, 1.23MB/s]
  8%|██▊                                  | 1.38M/18.3M [00:01<00:13, 1.21MB/s]
  8%|███                                  | 1.50M/18.3M [00:01<00:13, 1.20MB/s]
  9%|███▎                                  | 1.62M/18.3M [00:01<00:18, 917kB/s]
  9%|███▌                                  | 1.72M/18.3M [00:01<00:17, 934kB/s]
 10%|███▊                                  | 1.82M/18.3M [00:02<00:17, 944kB/s]
 11%|████                                  | 1.92M/18.3M [00:02<00:17, 951kB/s]
 11%|████▏                                 | 2.02M/18.3M [00:02<00:17, 953kB/s]
 12%|████▍                                 | 2.12M/18.3M [00:02<00:16, 951kB/s]
 12%|████▌                                 | 2.22M/18.3M [00:02<00:16, 947kB/s]
 13%|████▊                                 | 2.31M/18.3M [00:02<00:16, 943kB/s]
 13%|█████                                 | 2.42M/18.3M [00:02<00:16, 966kB/s]
 14%|█████▏                                | 2.52M/18.3M [00:02<00:16, 962kB/s]
 14%|█████▍                                | 2.62M/18.3M [00:02<00:16, 955kB/s]
 15%|█████▋                                | 2.71M/18.3M [00:03<00:16, 942kB/s]
 15%|█████▊                                | 2.81M/18.3M [00:03<00:16, 951kB/s]
 16%|██████                                | 2.91M/18.3M [00:03<00:16, 943kB/s]
 16%|██████▎                               | 3.00M/18.3M [00:03<00:16, 936kB/s]
 17%|██████▍                               | 3.10M/18.3M [00:03<00:16, 927kB/s]
 17%|██████▋                               | 3.19M/18.3M [00:03<00:16, 917kB/s]
 18%|██████▊                               | 3.28M/18.3M [00:03<00:16, 907kB/s]
 18%|███████                               | 3.38M/18.3M [00:03<00:16, 898kB/s]
 19%|███████▏                              | 3.47M/18.3M [00:03<00:16, 892kB/s]
 20%|███████▎                             | 3.60M/18.3M [00:03<00:14, 1.00MB/s]
 21%|███████▌                             | 3.74M/18.3M [00:04<00:12, 1.13MB/s]
 21%|███████▊                             | 3.86M/18.3M [00:04<00:12, 1.12MB/s]
 22%|████████                             | 3.97M/18.3M [00:04<00:12, 1.11MB/s]
 22%|████████▎                            | 4.08M/18.3M [00:04<00:12, 1.10MB/s]
 23%|████████▍                            | 4.19M/18.3M [00:04<00:12, 1.09MB/s]
 24%|████████▋                            | 4.30M/18.3M [00:04<00:12, 1.08MB/s]
 24%|████████▉                            | 4.41M/18.3M [00:04<00:12, 1.07MB/s]
 25%|█████████▏                           | 4.52M/18.3M [00:04<00:12, 1.06MB/s]
 25%|█████████▎                           | 4.63M/18.3M [00:04<00:12, 1.05MB/s]
 26%|█████████▌                           | 4.73M/18.3M [00:04<00:12, 1.04MB/s]
 26%|█████████▊                           | 4.84M/18.3M [00:05<00:13, 1.03MB/s]
 27%|██████████                           | 4.94M/18.3M [00:05<00:13, 1.02MB/s]
 28%|██████████▍                           | 5.04M/18.3M [00:05<00:16, 780kB/s]
 28%|██████████▋                           | 5.13M/18.3M [00:05<00:16, 794kB/s]
 29%|██████████▉                           | 5.23M/18.3M [00:05<00:15, 847kB/s]
 29%|███████████▏                          | 5.35M/18.3M [00:05<00:14, 915kB/s]
 30%|███████████▎                          | 5.45M/18.3M [00:05<00:13, 924kB/s]
 31%|███████████▎                         | 5.58M/18.3M [00:05<00:12, 1.02MB/s]
 31%|███████████▌                         | 5.71M/18.3M [00:06<00:11, 1.09MB/s]
 32%|███████████▊                         | 5.82M/18.3M [00:06<00:11, 1.08MB/s]
 32%|████████████                         | 5.93M/18.3M [00:06<00:11, 1.08MB/s]
 33%|████████████▏                        | 6.04M/18.3M [00:06<00:11, 1.07MB/s]
 34%|████████████▍                        | 6.15M/18.3M [00:06<00:11, 1.06MB/s]
 34%|████████████▋                        | 6.25M/18.3M [00:06<00:11, 1.05MB/s]
 35%|████████████▉                        | 6.36M/18.3M [00:06<00:11, 1.05MB/s]
 35%|█████████████                        | 6.47M/18.3M [00:06<00:11, 1.04MB/s]
 36%|█████████████▎                       | 6.57M/18.3M [00:06<00:11, 1.03MB/s]
 37%|█████████████▌                       | 6.67M/18.3M [00:06<00:11, 1.02MB/s]
 37%|█████████████▋                       | 6.78M/18.3M [00:07<00:11, 1.01MB/s]
 38%|██████████████▎                       | 6.88M/18.3M [00:07<00:11, 999kB/s]
 38%|██████████████▌                       | 6.98M/18.3M [00:07<00:11, 990kB/s]
 39%|██████████████▋                       | 7.08M/18.3M [00:07<00:11, 981kB/s]
 39%|██████████████▉                       | 7.18M/18.3M [00:07<00:11, 971kB/s]
 40%|███████████████▏                      | 7.27M/18.3M [00:07<00:11, 957kB/s]
 40%|███████████████▎                      | 7.37M/18.3M [00:07<00:11, 946kB/s]
 41%|███████████████▏                     | 7.49M/18.3M [00:07<00:10, 1.01MB/s]
 42%|███████████████▊                      | 7.59M/18.3M [00:07<00:10, 994kB/s]
 42%|████████████████                      | 7.69M/18.3M [00:07<00:10, 986kB/s]
 43%|███████████████▊                     | 7.80M/18.3M [00:08<00:10, 1.01MB/s]
 43%|████████████████▍                     | 7.90M/18.3M [00:08<00:10, 996kB/s]
 44%|████████████████▋                     | 8.00M/18.3M [00:08<00:10, 989kB/s]
 44%|████████████████▊                     | 8.10M/18.3M [00:08<00:10, 979kB/s]
 45%|█████████████████                     | 8.20M/18.3M [00:08<00:10, 969kB/s]
 45%|█████████████████▎                    | 8.30M/18.3M [00:08<00:10, 960kB/s]
 46%|█████████████████▍                    | 8.40M/18.3M [00:08<00:10, 983kB/s]
 47%|█████████████████▋                    | 8.50M/18.3M [00:08<00:10, 975kB/s]
 47%|█████████████████▉                    | 8.60M/18.3M [00:08<00:09, 966kB/s]
 48%|██████████████████                    | 8.70M/18.3M [00:09<00:09, 957kB/s]
 48%|██████████████████▎                   | 8.81M/18.3M [00:09<00:09, 998kB/s]
 49%|██████████████████▏                  | 8.95M/18.3M [00:09<00:08, 1.08MB/s]
 50%|██████████████████▎                  | 9.06M/18.3M [00:09<00:08, 1.07MB/s]
 50%|██████████████████▌                  | 9.16M/18.3M [00:09<00:08, 1.06MB/s]
 51%|██████████████████▊                  | 9.27M/18.3M [00:09<00:08, 1.05MB/s]
 51%|██████████████████▉                  | 9.38M/18.3M [00:09<00:08, 1.04MB/s]
 52%|███████████████████▏                 | 9.48M/18.3M [00:09<00:08, 1.03MB/s]
 52%|███████████████████▍                 | 9.58M/18.3M [00:09<00:08, 1.02MB/s]
 53%|████████████████████▏                 | 9.69M/18.3M [00:10<00:09, 932kB/s]
 54%|████████████████████▍                 | 9.81M/18.3M [00:10<00:08, 998kB/s]
 54%|████████████████████                 | 9.93M/18.3M [00:10<00:08, 1.03MB/s]
 55%|████████████████████▎                | 10.0M/18.3M [00:10<00:07, 1.05MB/s]
 56%|████████████████████▌                | 10.1M/18.3M [00:10<00:07, 1.04MB/s]
 56%|████████████████████▊                | 10.3M/18.3M [00:10<00:07, 1.04MB/s]
 57%|████████████████████▉                | 10.4M/18.3M [00:10<00:07, 1.03MB/s]
 57%|█████████████████████▏               | 10.5M/18.3M [00:10<00:07, 1.02MB/s]
 58%|█████████████████████▍               | 10.6M/18.3M [00:10<00:07, 1.01MB/s]
 58%|█████████████████████▌               | 10.7M/18.3M [00:10<00:07, 1.00MB/s]
 59%|██████████████████████▍               | 10.8M/18.3M [00:11<00:07, 991kB/s]
 60%|██████████████████████▌               | 10.9M/18.3M [00:11<00:07, 981kB/s]
 60%|██████████████████████▊               | 11.0M/18.3M [00:11<00:07, 971kB/s]
 61%|███████████████████████               | 11.1M/18.3M [00:11<00:07, 962kB/s]
 61%|███████████████████████▏              | 11.2M/18.3M [00:11<00:07, 952kB/s]
 62%|███████████████████████▍              | 11.3M/18.3M [00:11<00:07, 942kB/s]
 62%|███████████████████████▌              | 11.3M/18.3M [00:11<00:07, 929kB/s]
 63%|███████████████████████▊              | 11.4M/18.3M [00:11<00:07, 918kB/s]
 63%|████████████████████████              | 11.5M/18.3M [00:11<00:07, 948kB/s]
 64%|████████████████████████▏             | 11.6M/18.3M [00:11<00:06, 946kB/s]
 64%|████████████████████████▍             | 11.7M/18.3M [00:12<00:06, 935kB/s]
 65%|████████████████████████▋             | 11.8M/18.3M [00:12<00:06, 927kB/s]
 65%|████████████████████████▊             | 11.9M/18.3M [00:12<00:06, 907kB/s]
 66%|█████████████████████████             | 12.0M/18.3M [00:12<00:06, 954kB/s]
 66%|█████████████████████████▏            | 12.1M/18.3M [00:12<00:06, 946kB/s]
 67%|█████████████████████████▍            | 12.2M/18.3M [00:12<00:06, 938kB/s]
 67%|█████████████████████████▋            | 12.3M/18.3M [00:12<00:06, 929kB/s]
 68%|█████████████████████████▊            | 12.4M/18.3M [00:12<00:06, 919kB/s]
 68%|██████████████████████████            | 12.5M/18.3M [00:12<00:06, 910kB/s]
 69%|██████████████████████████▏           | 12.6M/18.3M [00:13<00:06, 900kB/s]
 69%|██████████████████████████▍           | 12.7M/18.3M [00:13<00:06, 890kB/s]
 70%|██████████████████████████▌           | 12.8M/18.3M [00:13<00:06, 881kB/s]
 70%|██████████████████████████▊           | 12.9M/18.3M [00:13<00:06, 874kB/s]
 71%|██████████████████████████▉           | 13.0M/18.3M [00:13<00:06, 867kB/s]
 71%|███████████████████████████▏          | 13.0M/18.3M [00:13<00:06, 858kB/s]
 72%|███████████████████████████▎          | 13.1M/18.3M [00:13<00:05, 861kB/s]
 72%|███████████████████████████▌          | 13.2M/18.3M [00:13<00:05, 854kB/s]
 73%|███████████████████████████▋          | 13.3M/18.3M [00:13<00:05, 865kB/s]
 73%|███████████████████████████▉          | 13.4M/18.3M [00:13<00:05, 890kB/s]
 74%|████████████████████████████▏         | 13.5M/18.3M [00:14<00:04, 952kB/s]
 75%|███████████████████████████▋         | 13.7M/18.3M [00:14<00:04, 1.09MB/s]
 75%|███████████████████████████▉         | 13.8M/18.3M [00:14<00:04, 1.08MB/s]
 76%|████████████████████████████▏        | 13.9M/18.3M [00:14<00:04, 1.07MB/s]
 77%|████████████████████████████▎        | 14.0M/18.3M [00:14<00:04, 1.06MB/s]
 77%|████████████████████████████▌        | 14.1M/18.3M [00:14<00:03, 1.05MB/s]
 78%|████████████████████████████▊        | 14.2M/18.3M [00:14<00:03, 1.04MB/s]
 78%|█████████████████████████████        | 14.3M/18.3M [00:14<00:03, 1.03MB/s]
 79%|█████████████████████████████▏       | 14.4M/18.3M [00:14<00:03, 1.02MB/s]
 80%|█████████████████████████████▍       | 14.5M/18.3M [00:14<00:03, 1.01MB/s]
 80%|█████████████████████████████▋       | 14.6M/18.3M [00:15<00:03, 1.00MB/s]
 81%|██████████████████████████████▋       | 14.7M/18.3M [00:15<00:04, 763kB/s]
 81%|██████████████████████████████▊       | 14.8M/18.3M [00:15<00:04, 777kB/s]
 82%|███████████████████████████████       | 14.9M/18.3M [00:15<00:04, 800kB/s]
 82%|███████████████████████████████▏      | 15.0M/18.3M [00:15<00:03, 840kB/s]
 83%|███████████████████████████████▍      | 15.1M/18.3M [00:15<00:03, 870kB/s]
 83%|███████████████████████████████▌      | 15.2M/18.3M [00:15<00:03, 892kB/s]
 84%|███████████████████████████████▊      | 15.3M/18.3M [00:15<00:03, 905kB/s]
 84%|████████████████████████████████      | 15.4M/18.3M [00:16<00:02, 964kB/s]
 85%|████████████████████████████████▎     | 15.5M/18.3M [00:16<00:02, 958kB/s]
 86%|███████████████████████████████▋     | 15.7M/18.3M [00:16<00:02, 1.10MB/s]
 86%|███████████████████████████████▉     | 15.8M/18.3M [00:16<00:02, 1.09MB/s]
 87%|████████████████████████████████▏    | 15.9M/18.3M [00:16<00:02, 1.08MB/s]
 88%|████████████████████████████████▍    | 16.0M/18.3M [00:16<00:02, 1.06MB/s]
 88%|████████████████████████████████▌    | 16.1M/18.3M [00:16<00:02, 1.06MB/s]
 89%|████████████████████████████████▊    | 16.2M/18.3M [00:16<00:01, 1.05MB/s]
 89%|█████████████████████████████████    | 16.3M/18.3M [00:16<00:01, 1.06MB/s]
 90%|█████████████████████████████████▎   | 16.4M/18.3M [00:16<00:01, 1.12MB/s]
 91%|█████████████████████████████████▌   | 16.5M/18.3M [00:17<00:01, 1.10MB/s]
 91%|█████████████████████████████████▊   | 16.7M/18.3M [00:17<00:01, 1.09MB/s]
 92%|█████████████████████████████████▉   | 16.8M/18.3M [00:17<00:01, 1.08MB/s]
 92%|██████████████████████████████████▏  | 16.9M/18.3M [00:17<00:01, 1.07MB/s]
 93%|██████████████████████████████████▍  | 17.0M/18.3M [00:17<00:01, 1.06MB/s]
 94%|██████████████████████████████████▋  | 17.1M/18.3M [00:17<00:01, 1.05MB/s]
 94%|██████████████████████████████████▊  | 17.2M/18.3M [00:17<00:01, 1.04MB/s]
 95%|███████████████████████████████████  | 17.3M/18.3M [00:17<00:00, 1.03MB/s]
 95%|███████████████████████████████████▎ | 17.4M/18.3M [00:17<00:00, 1.02MB/s]
 96%|███████████████████████████████████▍ | 17.5M/18.3M [00:18<00:00, 1.01MB/s]
 96%|███████████████████████████████████▋ | 17.6M/18.3M [00:18<00:00, 1.00MB/s]
 97%|████████████████████████████████████▊ | 17.7M/18.3M [00:18<00:00, 990kB/s]
 98%|█████████████████████████████████████ | 17.8M/18.3M [00:18<00:00, 981kB/s]
 98%|█████████████████████████████████████▎| 17.9M/18.3M [00:18<00:00, 971kB/s]
 99%|█████████████████████████████████████▍| 18.0M/18.3M [00:18<00:00, 963kB/s]
 99%|█████████████████████████████████████▋| 18.1M/18.3M [00:18<00:00, 955kB/s]
100%|█████████████████████████████████████▊| 18.2M/18.3M [00:18<00:00, 947kB/s]
  0%|                                              | 0.00/18.3M [00:00<?, ?B/s]
100%|██████████████████████████████████████| 18.3M/18.3M [00:00<00:00, 123GB/s]

Using Manual Ellipse Determination#

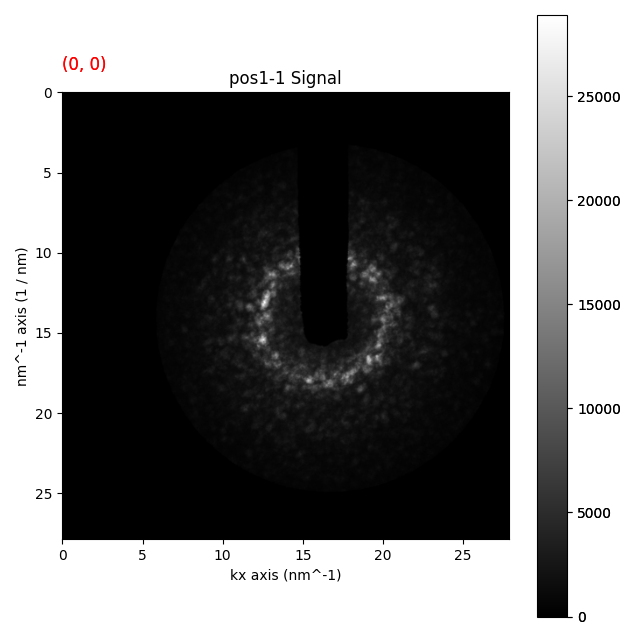
Sometimes it is useful to force the ellipse to fit certain points. For example, here we can force the ellipse to fit the first ring by masking the zero beam.

summed = s.sum()

center, affine, params, pos = pxm.utils.ransac_ellipse_tools.determine_ellipse(
    summed,
    return_params=True,
    num_points=500,
    use_ransac=False,
)
el, in_points = pxm.utils.ransac_ellipse_tools.ellipse_to_markers(
    ellipse_array=params,
    points=pos,
)

# we don't account for scales/offsets yet
summed.axes_manager.signal_axes[0].scale = 1
summed.axes_manager.signal_axes[1].scale = 1
summed.axes_manager.signal_axes[1].offset = 0
summed.axes_manager.signal_axes[0].offset = 0

Checking#

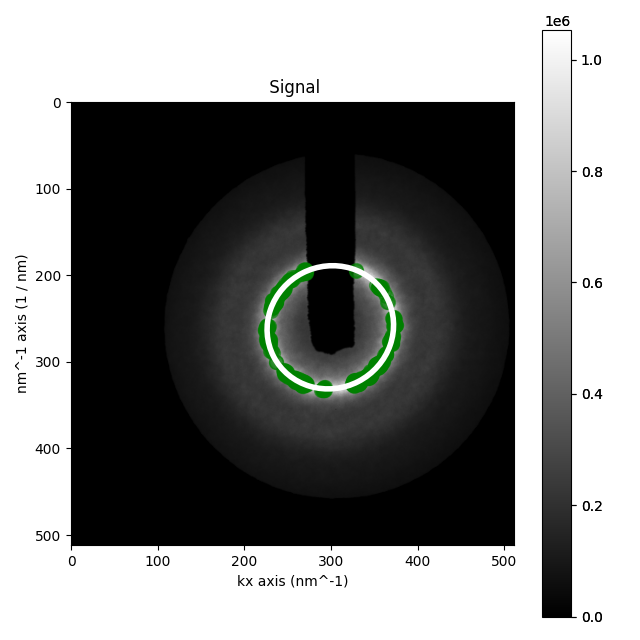
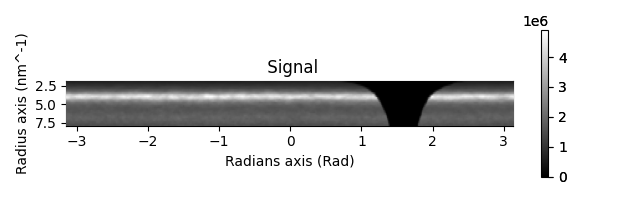
Let’s check to make sure that things are behaving. We can first plot the ellipse over the data and then take the azimuthal integral/sum. That should end up a nice straight line

summed.plot()
summed.add_marker(in_points, plot_marker=True)
summed.add_marker(el, plot_marker=True)


s.calibration.center = center[::-1]  # reverse the center.
s.calibration.affine = affine
az = s.get_azimuthal_integral2d(npt=100).sum().isig[:, 2.0:8.0]

az.sum().plot()

  0%|          | 0/17 [00:00<?, ?it/s]
  6%|▌         | 1/17 [00:03<01:00,  3.77s/it]
 65%|██████▍   | 11/17 [00:03<00:01,  3.88it/s]
100%|██████████| 17/17 [00:03<00:00,  4.30it/s]

Getting the Variance#

The get_variance() function will calculate the variance using the affine correction and the center as described above. Restricting the radial range is also nice to remove the effects of the high intensity at the top end. Adding a mask can also be helpful for reducing the effects of a beam stop. The gain parameter is number of detector units for 1 electron. It’s used for the Poisson noise correction. If the data are already calibrated in units of electron counts, use a gain of 1.

mask = summed < 10000
mask.plot()
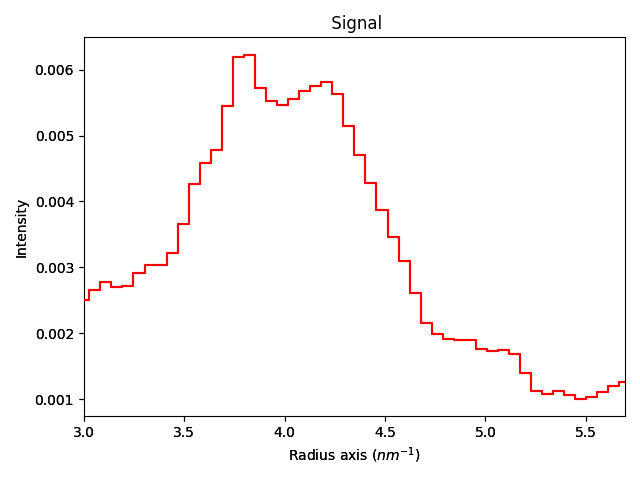
variance = s.get_variance(npt=50, gain=4.2, radial_range=(3.0, 5.75), mask=mask)
variance.axes_manager[0].units = "$nm^{-1}$"
variance.plot()

  0%|          | 0/33 [00:00<?, ?it/s]
  3%|▎         | 1/33 [00:00<00:10,  2.96it/s]
100%|██████████| 33/33 [00:00<00:00, 77.29it/s]

  0%|          | 0/33 [00:00<?, ?it/s]
  3%|▎         | 1/33 [00:00<00:08,  3.97it/s]
100%|██████████| 33/33 [00:00<00:00, 106.03it/s]

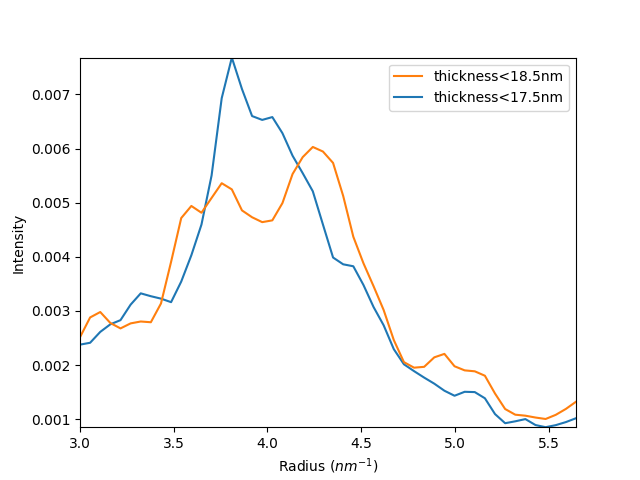
Getting a (Good) Variance#

If the TEM sample varies in thickness by more than a few nm over the entire dataset, thickness-related differences in the diffracted intensity will dominate structure-related differences and therefore dominate. This effect can be avoided by using the HAADF signal or the high-angle scattering within the diffraction pattern to determine the local sample thickness, grouping the diffraction patterns into bins of nearly constant thickness, and only computing \(V_\\Omega (k)\) for data inside a single bin. The \(V_\\Omega (k)\) from different thickness bins then can be averaged together. See Hwang and Voyles Microscopy and Microanalysis 17, 67–74 (2011), DOI: 10.1017/S1431927610094109 and Li et al. Microscopy and Microanalysis 20, 1605–1618 (2014). DOI: 10.1017/s1431927614012756 for more details.

# We have already saved the simultaneously-acquired HAADF image along side the dataset. We can see this here...
haadf = s.metadata.HAADF.intensity

The HAADF signal for an amorphous material is linear in the thickness for typical TEM sample thicknesses. To convert the HAADF digital counts to thickness (in e.g. nm), the slope and intercept of the linear relationship must be known. The intercept is the black level of the HAADF detector in digital counts, which in this case is 26,265. The slope must be calibrated for each experiment from a measurement of the HAADF intensity at a position of known sample thickness. In this case, the slope is 440.46 digital counts / nm of sample thickness.

TEM sample thickness for amorphous materials can be measured independently either using electron energy loss spectroscopy (EELS), in which the inelastic mean free path of the material must be known, or using total elastic scattering, in which case the elastic mean free path of the material must be known. A reasonable model for the elastic mean free path for many inorganic materials may be found in Zhang et al. Ultramicroscopy 171, 89–95 (2016), DOI: 10.1016/j.ultramic.2016.09.005.

thickness = (haadf - 26265) / 440.46


def thickness_filter(signal, thickness, bins):
    masks = [
        np.logical_and(bins[i] < thickness, bins[i + 1] > thickness)
        for i in range(len(bins) - 1)
    ]
    filtered = [hs.signals.Signal2D(signal.data[m.data, :, :]) for m in masks]
    for f in filtered:
        f.set_signal_type("electron_diffraction")
        _copy_axes_object_metadata(
            signal.axes_manager.signal_axes[0], f.axes_manager.signal_axes[0]
        )
        _copy_axes_object_metadata(
            signal.axes_manager.signal_axes[1], f.axes_manager.signal_axes[1]
        )
        f.metadata.add_dictionary(signal.metadata.as_dictionary())
    return filtered, thickness


bins = np.linspace(
    np.min(thickness, axis=(0, 1)), np.max(thickness, axis=(0, 1)), num=2 + 1
)
filtered, thickness = thickness_filter(s, thickness, bins)
var = [
    f.get_variance(npt=50, gain=4.2, radial_range=(3.0, 5.7), mask=mask)
    for f in filtered
]

# Note that the y-axis is the variance here. Hyperspy just always labels this as "Intensity"
for v in var:
    v.axes_manager[0].units = "$nm^{-1}$"
hs.plot.plot_spectra(var, legend=["thickness<17.5nm", "thickness<18.5nm"])

  0%|          | 0/25 [00:00<?, ?it/s]
100%|██████████| 25/25 [00:00<00:00, 563.39it/s]

  0%|          | 0/25 [00:00<?, ?it/s]
100%|██████████| 25/25 [00:00<00:00, 824.38it/s]

  0%|          | 0/21 [00:00<?, ?it/s]
100%|██████████| 21/21 [00:00<00:00, 458.12it/s]

  0%|          | 0/21 [00:00<?, ?it/s]
100%|██████████| 21/21 [00:00<00:00, 681.20it/s]

<Axes: xlabel='Radius ($nm^{-1}$)', ylabel='Intensity'>

Total running time of the script: (0 minutes 51.819 seconds)

Gallery generated by Sphinx-Gallery